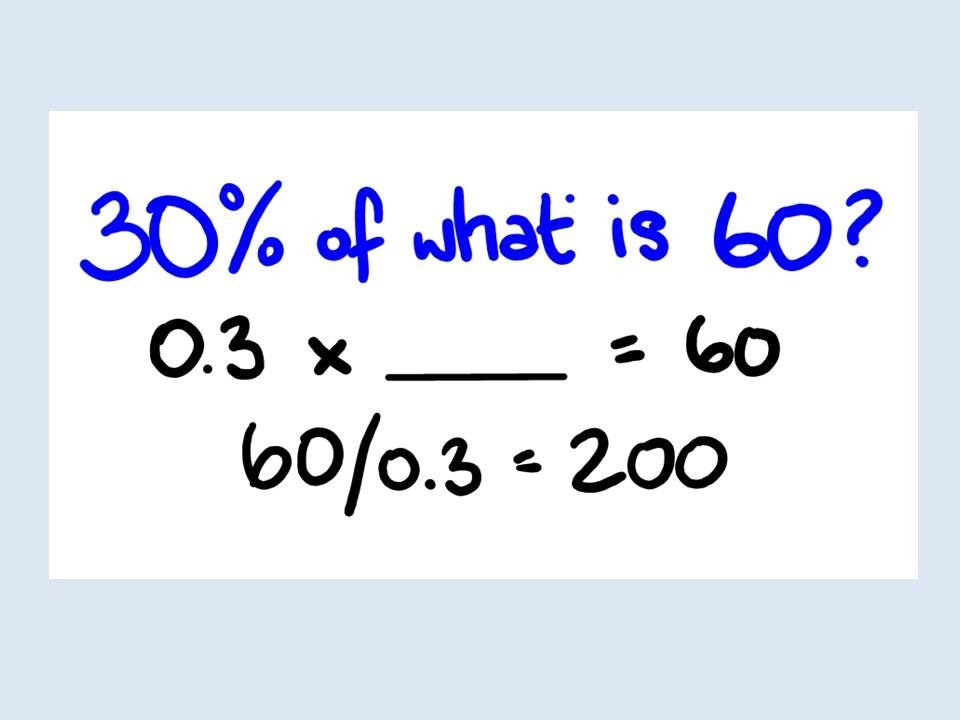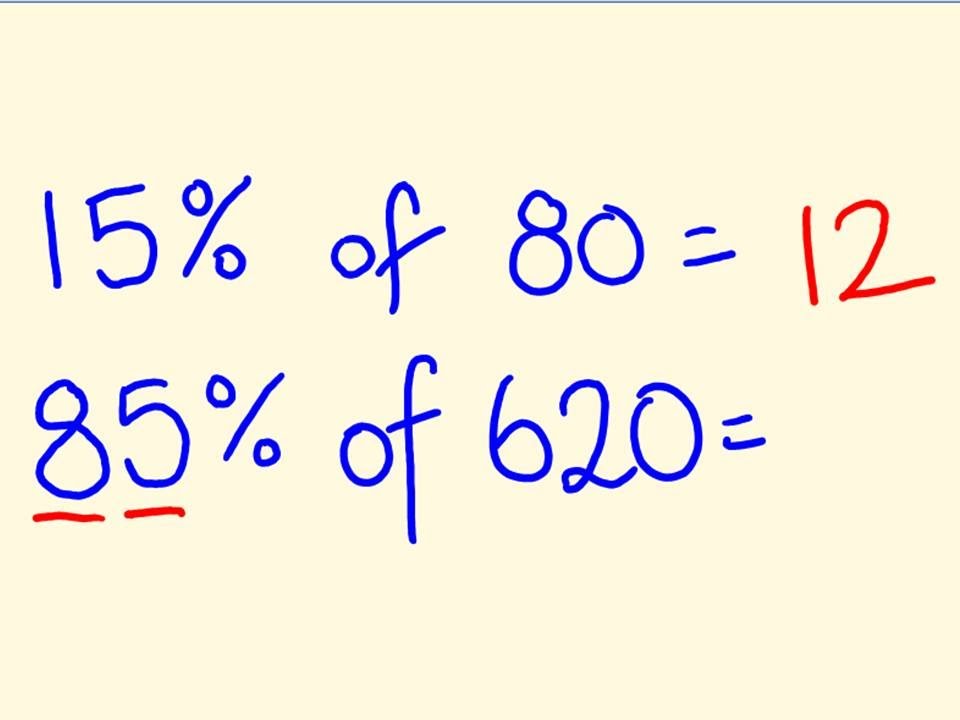How to find 80 percent of a number? This seemingly simple question is one that often arises in various situations, from calculating discounts during a shopping spree to determining the portion of a budget allocated for a specific purpose. Whether you're a student grappling with mathematics or an adult navigating the financial aspects of daily life, knowing how to find 80 percent of a number is a valuable skill. It empowers us to make informed decisions and enhances our numerical literacy. But how do we go about it effectively and accurately?
The process of finding 80 percent of a number is not confined to the confines of a classroom. It's a practical skill that transcends academia and finds relevance in everyday activities. Understanding the concept of percentages and their application can demystify what might initially appear as a daunting task. In this comprehensive guide, we will delve into the methodical approach to calculating 80 percent of a number, ensuring you are equipped with the knowledge to tackle any percentage-related query with confidence.
Throughout this article, we will explore various methods and real-world applications, providing a well-rounded perspective on the topic. From basic arithmetic techniques to leveraging technology, the goal is to offer an accessible and thorough understanding of how to find 80 percent of a number. By the end, you will not only grasp the fundamental principles but also appreciate the versatility and practicality of percentages in diverse contexts.
Table of Contents
- Understanding Percentages
- Basic Mathematical Concepts
- Step-by-Step Guide to Finding 80 Percent
- Using Calculators for Accuracy
- Real-World Applications of 80 Percent Calculations
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Complex Calculations
- Technological Aids and Tools
- Educational Resources and Learning Aids
- Importance of Practice and Consistency
- Visual Representations of Percentages
- Case Studies: Real-Life Examples
- Frequently Asked Questions
- External Resources and Further Reading
- Conclusion
Understanding Percentages
Percentages are a fundamental aspect of mathematics, representing a portion of a whole as a fraction of 100. The term "percent" originates from the Latin "per centum," meaning "by the hundred." Understanding percentages is crucial because they are used to express proportions, compare quantities, and calculate changes in values. They simplify complex numerical relationships, making them easier to interpret and communicate.
At its core, a percentage is a way to express a number as a part of a whole. In the context of finding 80 percent of a number, the percentage indicates that you are looking for 80 parts out of 100 of the given number. This understanding is crucial as it lays the foundation for accurate calculations and interpretations.
Historical Context of Percentages
The concept of percentages has a rich history, tracing back to ancient civilizations that used fractions and ratios to solve problems related to trade and commerce. Over time, the use of percentages became more standardized, particularly during the Renaissance when European mathematicians began to formalize mathematical concepts. Today, percentages are a ubiquitous part of everyday life, from calculating interest rates to understanding statistics in media reports.
Why Percentages Matter
Percentages are vital because they provide a universal language for comparing quantities. In financial terms, they help individuals understand interest rates, investment returns, and inflation. In health and science, percentages are used to communicate data such as vaccination rates and statistical probabilities. By grasping the concept of percentages, individuals can make informed decisions based on accurate data analysis.
Basic Mathematical Concepts
Before diving into the process of finding 80 percent of a number, it's essential to revisit some basic mathematical concepts that underpin percentage calculations. These include understanding fractions, decimals, and their interconversion, as well as basic arithmetic operations such as multiplication and division.
Fractions and Decimals
Fractions and decimals are two ways of expressing parts of a whole. A fraction consists of a numerator and a denominator, representing a division of the numerator by the denominator. For example, 80 percent can be expressed as the fraction 80/100, which simplifies to 4/5. Decimals, on the other hand, express numbers in base ten, making them particularly useful for calculations involving percentages.
Interconverting Fractions, Decimals, and Percentages
To convert a fraction to a percentage, multiply it by 100. Conversely, to convert a percentage to a fraction, divide it by 100 and simplify if necessary. For example, converting 80 percent to a fraction involves dividing 80 by 100, resulting in 4/5. Similarly, converting a decimal to a percentage involves multiplying the decimal by 100. Understanding these conversions is crucial for performing accurate percentage calculations.
Step-by-Step Guide to Finding 80 Percent
Finding 80 percent of a number involves a straightforward arithmetic process. This section provides a step-by-step guide to ensure accuracy and clarity in calculations. Whether you're using mental math or a calculator, following these steps will help you arrive at the correct answer.
Step 1: Understanding the Number
The first step is to identify the number from which you want to find 80 percent. This could be any numerical value, such as a price, a quantity, or a measurement. Understanding the context of the number is important as it provides meaning to the percentage calculation.
Step 2: Converting the Percentage to a Decimal
To facilitate easier calculations, convert the percentage to a decimal. For 80 percent, divide 80 by 100, resulting in 0.8. This decimal representation allows you to perform multiplication operations easily.
Step 3: Performing the Multiplication
Multiply the decimal obtained in Step 2 by the number identified in Step 1. This multiplication will give you 80 percent of the number. For example, if the number is 50, multiplying 50 by 0.8 yields 40, which is 80 percent of 50.
Step 4: Verifying the Result
After performing the calculation, it's always a good idea to verify the result. You can do this by using a different method or a calculator to ensure accuracy. Verification is especially important in real-world scenarios where precision is crucial.
Using Calculators for Accuracy
While mental math is a valuable skill, calculators provide a reliable and efficient tool for performing percentage calculations. They eliminate the possibility of human error and ensure accuracy, especially when dealing with large or complex numbers.
Types of Calculators
There are various types of calculators available, ranging from basic handheld devices to advanced scientific calculators and online tools. Each has its own set of features and capabilities, allowing users to choose based on their specific needs and preferences.
How to Use a Calculator for Percentage Calculations
Using a calculator to find 80 percent of a number involves entering the number, multiplying it by 0.8, and observing the result. Most calculators have a percentage function that simplifies this process, allowing users to input the percentage directly and obtain the answer with minimal effort.
Advantages of Using Calculators
Calculators offer numerous advantages, including speed, accuracy, and convenience. They are particularly useful in situations where quick calculations are required, such as during exams or in professional settings. Additionally, calculators help individuals verify manual calculations, ensuring that errors are caught and corrected.
Real-World Applications of 80 Percent Calculations
Understanding how to find 80 percent of a number has practical applications in various aspects of daily life. This section explores some of the common scenarios where percentage calculations are used, highlighting their relevance and importance.
Shopping and Discounts
One of the most common applications of percentage calculations is in shopping, particularly when determining discounts. Retailers often offer discounts expressed as percentages, such as 20 percent off or 80 percent of the original price. Being able to calculate these discounts allows consumers to make informed purchasing decisions and maximize savings.
Budgeting and Financial Planning
In financial planning, percentages are used to allocate portions of a budget to different categories, such as savings, expenses, and investments. For example, if a person wants to save 80 percent of a bonus, they need to calculate 80 percent of the bonus amount to determine the savings portion.
Health and Nutrition
In health and nutrition, percentages are used to express data such as the percentage of daily recommended nutrient intake. For instance, a nutrition label might indicate that a food item provides 80 percent of the recommended daily intake of vitamin C, helping individuals make dietary choices aligned with their health goals.
Common Mistakes and How to Avoid Them
While finding 80 percent of a number is a straightforward process, there are common mistakes that individuals might encounter. Understanding these pitfalls and how to avoid them is crucial for accurate calculations and interpretations.
Mistake 1: Incorrect Conversion of Percentages
One common mistake is incorrectly converting percentages to decimals. For example, forgetting to divide by 100 can lead to incorrect results. To avoid this, always double-check the conversion process and ensure that the percentage is accurately represented as a decimal.
Mistake 2: Misinterpretation of the Number
Another mistake is misinterpreting the number from which the percentage is being calculated. It's important to clearly define the number and its context to ensure that the percentage calculation is meaningful and relevant.
Mistake 3: Rounding Errors
Rounding errors can occur when dealing with decimals, especially in cases where precise measurements are required. To avoid rounding errors, consider using a calculator with sufficient decimal places and verify calculations through multiple methods if necessary.
Strategies for Avoiding Mistakes
To minimize the likelihood of mistakes, practice consistently, verify calculations through multiple methods, and use tools or calculators when necessary. Additionally, understanding the underlying concepts and processes will enhance accuracy and confidence in percentage calculations.
Advanced Techniques for Complex Calculations
While basic percentage calculations are straightforward, there are advanced techniques that can be applied to more complex scenarios. These techniques involve the use of algebraic expressions, ratios, and proportions to solve percentage-related problems.
Using Algebraic Expressions
Algebraic expressions provide a powerful tool for solving complex percentage problems. By representing unknowns as variables and setting up equations, individuals can solve for specific values and gain insights into numerical relationships.
Applying Ratios and Proportions
Ratios and proportions are useful for comparing quantities and determining relationships between numbers. By setting up proportions, individuals can solve for unknowns and gain a deeper understanding of percentage relationships.
Leveraging Statistical Methods
In situations where percentages are used to analyze data, statistical methods can provide valuable insights. Techniques such as regression analysis and hypothesis testing allow individuals to interpret data and draw meaningful conclusions based on percentage relationships.
Technological Aids and Tools
In addition to calculators, there are various technological aids and tools that can assist individuals in percentage calculations. These tools range from mobile apps to online platforms, offering convenience and efficiency in performing calculations and interpreting results.
Mobile Apps
Mobile apps provide a convenient way to perform percentage calculations on the go. Many apps offer user-friendly interfaces and additional features, such as graphing and data analysis, to enhance the calculation process.
Online Platforms
Online platforms offer a wide range of tools and resources for percentage calculations. These platforms often include calculators, tutorials, and interactive exercises to support learning and application of percentage concepts.
Software Programs
Software programs, such as spreadsheet applications, provide powerful tools for performing complex calculations and data analysis. These programs allow users to automate calculations, visualize data, and generate reports, making them valuable for professional and academic settings.
Educational Resources and Learning Aids
For those seeking to deepen their understanding of percentages and improve their calculation skills, there are numerous educational resources and learning aids available. These resources cater to different learning styles and preferences, providing valuable support for learners at all levels.
Textbooks and Workbooks
Textbooks and workbooks offer structured learning materials that cover the fundamentals of percentages and provide practice exercises for skill development. These resources are often used in educational settings to facilitate learning and reinforce concepts.
Online Courses and Tutorials
Online courses and tutorials provide flexible learning opportunities for individuals seeking to enhance their percentage calculation skills. These resources often include video content, interactive exercises, and assessments to support learning and application of concepts.
Interactive Simulations
Interactive simulations offer engaging and immersive learning experiences that allow individuals to explore percentage concepts in a virtual environment. These simulations often include real-world scenarios and problem-solving activities to enhance understanding and application of percentage concepts.
Importance of Practice and Consistency
Consistent practice is essential for mastering percentage calculations and building confidence in applying mathematical concepts. Regular practice helps individuals develop a deeper understanding of percentages and enhances their ability to perform accurate calculations in various contexts.
Building Confidence Through Practice
Practicing percentage calculations helps individuals build confidence in their mathematical abilities and reduces anxiety associated with numerical tasks. By engaging in regular practice, individuals can reinforce their understanding of concepts and improve their calculation skills.
Enhancing Problem-Solving Skills
Consistent practice enhances problem-solving skills by encouraging individuals to apply percentage concepts in diverse scenarios. This practice fosters critical thinking and analytical skills, allowing individuals to approach complex problems with confidence and creativity.
Visual Representations of Percentages
Visual representations, such as graphs and charts, provide a powerful tool for understanding and interpreting percentage data. These visual aids enhance comprehension and communication by presenting numerical information in an accessible and engaging format.
Types of Visual Representations
Common types of visual representations include pie charts, bar graphs, and line graphs. Each type of representation offers unique advantages and can be used to convey different aspects of percentage data, such as proportions, comparisons, and trends.
Benefits of Visual Representations
Visual representations offer several benefits, including enhanced comprehension, improved communication, and increased engagement. By presenting data visually, individuals can gain insights into numerical relationships and make informed decisions based on accurate interpretations of percentage data.
Case Studies: Real-Life Examples
To illustrate the practical applications of percentage calculations, this section presents case studies that highlight real-life examples. These case studies demonstrate how percentages are used in various contexts, from business and finance to health and education.
Case Study 1: Business and Finance
In the business world, percentages are used to calculate profit margins, analyze financial performance, and assess investment opportunities. This case study explores how a company uses percentage calculations to evaluate its financial health and make strategic decisions for growth and expansion.
Case Study 2: Health and Education
In the fields of health and education, percentages are used to assess outcomes, measure progress, and communicate data. This case study examines how an educational institution uses percentage calculations to evaluate student performance and implement data-driven improvements in teaching and learning.
Frequently Asked Questions
Here are some commonly asked questions about finding 80 percent of a number, along with clear and concise answers to enhance understanding and address common concerns.
What is the formula for finding 80 percent of a number?
The formula for finding 80 percent of a number is to multiply the number by 0.8. This multiplication yields the portion of the number that represents 80 percent.
Can I use a calculator to find 80 percent of a number?
Yes, calculators are a convenient and accurate tool for finding 80 percent of a number. Simply enter the number, multiply it by 0.8, and observe the result to obtain the percentage.
Why is it important to understand percentages?
Understanding percentages is important because they are used to express proportions, compare quantities, and calculate changes in values. They are a fundamental aspect of mathematics with practical applications in various fields.
How can I avoid common mistakes in percentage calculations?
To avoid common mistakes, practice consistently, verify calculations through multiple methods, and use tools or calculators when necessary. Understanding the underlying concepts and processes will also enhance accuracy and confidence.
Are there advanced techniques for complex percentage problems?
Yes, advanced techniques such as using algebraic expressions, ratios, and statistical methods can be applied to more complex percentage problems. These techniques provide valuable insights into numerical relationships and support data analysis.
What resources are available for learning about percentages?
There are numerous resources available for learning about percentages, including textbooks, online courses, interactive simulations, and mobile apps. These resources cater to different learning styles and preferences, providing valuable support for learners at all levels.
External Resources and Further Reading
For those interested in learning more about percentages and their applications, here are some external resources and further reading materials that offer valuable insights and information.
- Khan Academy: Introduction to Percentages
- Math is Fun: Percentages
- Investopedia: Percentage Definition and Applications
Conclusion
In conclusion, understanding how to find 80 percent of a number is a valuable skill with practical applications in various aspects of daily life. From shopping and budgeting to health and education, percentages provide a universal language for comparing quantities and making informed decisions. By mastering the basic concepts and techniques, individuals can enhance their numerical literacy and confidently navigate percentage-related challenges. Through consistent practice, exploration of advanced techniques, and utilization of technological aids, the ability to calculate and interpret percentages becomes second nature, empowering individuals to thrive in a data-driven world.