Have you ever wondered how to construct a relative frequency distribution of the data? It's a critical skill in the realm of statistics and data analysis, allowing you to make sense of vast amounts of information by organizing it into a format that's easy to understand and interpret. Constructing a relative frequency distribution of the data is not just a task for statisticians or data scientists. It's a valuable tool for anyone looking to make informed decisions based on data. Whether you're a student, a business analyst, or a researcher, understanding how to effectively construct a relative frequency distribution can empower you to draw meaningful conclusions from the data at hand.
In today's data-driven world, the ability to interpret data accurately is more important than ever. A relative frequency distribution provides a snapshot of how often different values occur within a data set, helping to reveal patterns, trends, and anomalies. By constructing a relative frequency distribution of the data, you can easily compare different data sets, identify outliers, and make predictions based on historical data. This process involves not just counting occurrences but also considering the context of the data, providing a nuanced view that simple counts alone cannot offer.
Throughout this article, we'll delve into the step-by-step process of constructing a relative frequency distribution of the data. From the initial gathering of data to the final interpretation of results, each stage is crucial for ensuring the accuracy and reliability of your analysis. By the end of this guide, you'll have a comprehensive understanding of how to construct a relative frequency distribution of the data, along with practical tips and insights to apply this knowledge in real-world scenarios. So, let's embark on this journey to master the art of data interpretation and unlock the potential within your data sets.
Table of Contents
- Understanding Relative Frequency
- Importance of Relative Frequency Distribution
- Steps to Construct Relative Frequency Distribution
- Gathering and Organizing Data
- Calculating Frequency
- Determining Total Frequency
- Calculating Relative Frequency
- Creating the Distribution Table
- Interpreting the Results
- Common Mistakes to Avoid
- Applications in Real-World Scenarios
- Advanced Techniques and Tools
- Case Study Analysis
- Frequently Asked Questions
- Conclusion
Understanding Relative Frequency
Relative frequency is a statistical measure that represents the ratio of the number of times a specific event occurs to the total number of trials or observations. It's expressed as a proportion or percentage and provides insights into the likelihood of certain outcomes within a data set. By focusing on relative frequency, analysts can gain a clearer understanding of the data's distribution, as it accounts for the size of the data set and allows for comparison across different data sets or categories.
When analyzing data, relative frequency helps to normalize the data, making it easier to interpret and compare. This is especially useful when dealing with large data sets where absolute frequencies can be overwhelming or misleading. By converting absolute frequencies into relative frequencies, you can identify patterns and trends more effectively, which can inform decision-making and strategic planning.
In essence, relative frequency is a foundational concept in statistics that enables data analysts to go beyond mere counts and explore the underlying dynamics of the data. It serves as a bridge between raw data and meaningful insights, facilitating a deeper comprehension of the data's behavior and implications.
Importance of Relative Frequency Distribution
Relative frequency distribution is a pivotal tool in data analysis, offering a structured approach to understanding how data points are distributed across different categories or intervals. By constructing a relative frequency distribution of the data, analysts can transform raw data into a visual format that highlights the relative importance or prevalence of each category within the data set.
This method is crucial for several reasons. First, it aids in identifying patterns and trends that may not be immediately apparent from raw data. For instance, in a sales data set, a relative frequency distribution can reveal which products are most popular among customers, guiding inventory and marketing decisions. Second, it allows for comparison between different data sets or groups, facilitating a more comprehensive analysis of relationships and differences.
Moreover, relative frequency distributions simplify the communication of complex data insights. By presenting data in a clear and concise format, analysts can effectively convey their findings to stakeholders, enabling informed decision-making that aligns with organizational goals. Overall, the ability to construct a relative frequency distribution of the data is an essential skill for anyone involved in data-driven decision-making.
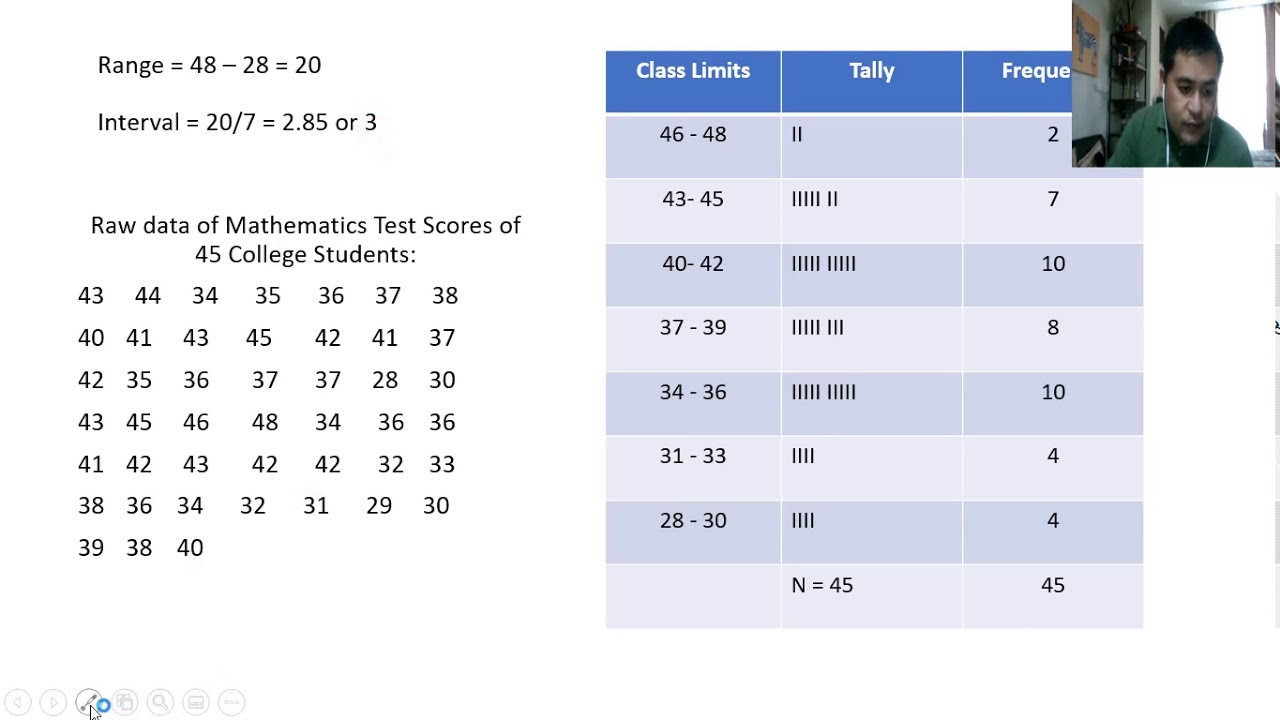
Steps to Construct Relative Frequency Distribution
Constructing a relative frequency distribution involves a systematic approach that transforms raw data into a meaningful representation of its distribution. The process can be broken down into several key steps, each of which plays a vital role in ensuring the accuracy and reliability of the final distribution. By following these steps, analysts can construct a relative frequency distribution of the data that effectively captures the essence of the data set.
Gathering and Organizing Data
The first step in constructing a relative frequency distribution is gathering and organizing the data. This involves collecting the data points that will be analyzed and arranging them in a format that facilitates further analysis. Depending on the nature of the data, this may involve sorting the data into categories or intervals, or simply listing the data points in a sequential order.
Calculating Frequency
Once the data is organized, the next step is to calculate the frequency of each category or interval. This involves counting the number of times each unique value or category appears within the data set. The resulting frequency counts provide a foundational understanding of how the data is distributed, serving as the basis for calculating relative frequencies.
Determining Total Frequency
After calculating the frequency of each category, the total frequency must be determined. This is achieved by summing all the individual frequency counts, resulting in a single value that represents the total number of data points within the data set. This total frequency is crucial for calculating relative frequencies, as it provides the denominator in the relative frequency formula.
Calculating Relative Frequency
With the individual frequencies and the total frequency in hand, the relative frequency for each category can be calculated. This is done by dividing the frequency of each category by the total frequency, resulting in a proportion or percentage that represents the relative importance of each category within the data set. The relative frequency provides a standardized measure that allows for easy comparison across categories.
Creating the Distribution Table
The final step in constructing a relative frequency distribution is creating the distribution table. This table presents the relative frequencies for each category in a clear and concise format, often accompanied by additional information such as cumulative frequencies or visual aids like bar charts or histograms. The distribution table serves as the primary tool for interpreting and communicating the results of the analysis.
Interpreting the Results
Interpreting the results of a relative frequency distribution requires a keen eye for detail and a solid understanding of the data's context. The distribution table provides a wealth of information, revealing not only the relative importance of each category but also potential patterns, trends, and outliers. By carefully analyzing these elements, analysts can draw meaningful conclusions that inform decision-making and strategy development.
For example, in a sales data set, a relative frequency distribution might reveal which products are most popular, indicating areas for potential expansion or increased marketing efforts. Similarly, in an academic setting, a relative frequency distribution of exam scores can highlight areas where students may need additional support or resources. By interpreting the distribution in light of the data's context, analysts can uncover valuable insights that drive informed decision-making.
Common Mistakes to Avoid
While constructing a relative frequency distribution can provide valuable insights, it's important to be aware of common mistakes that can compromise the accuracy and reliability of the analysis. One common error is failing to properly organize the data before calculating frequencies, which can lead to inaccurate counts and skewed results. It's essential to ensure that data is categorized correctly and consistently before proceeding with the analysis.
Another common mistake is overlooking the importance of context when interpreting the results. While a relative frequency distribution provides a snapshot of how data points are distributed, it's crucial to consider the broader context in which the data was collected. This includes understanding any potential biases or limitations in the data set, as well as external factors that may influence the results.
Finally, it's important to avoid relying solely on relative frequency distributions for decision-making. While these distributions provide valuable insights, they should be used in conjunction with other analytical tools and techniques for a comprehensive understanding of the data. By being mindful of these common pitfalls, analysts can construct a relative frequency distribution of the data that accurately reflects the data set's distribution and supports informed decision-making.
Applications in Real-World Scenarios
The ability to construct a relative frequency distribution of the data has numerous applications across a wide range of fields and industries. In business, relative frequency distributions are used to analyze customer behavior, optimize inventory management, and inform marketing strategies. By understanding which products or services are most popular among customers, businesses can tailor their offerings to meet demand and maximize profitability.
In healthcare, relative frequency distributions can be used to analyze patient outcomes, track the prevalence of diseases, and evaluate the effectiveness of treatment plans. By examining how often certain health conditions occur within a population, healthcare providers can identify trends and allocate resources more effectively to address public health concerns.
In education, relative frequency distributions are used to assess student performance, identify areas for improvement, and develop targeted interventions to support student success. By analyzing exam scores or other performance metrics, educators can gain insights into student learning patterns and adjust teaching strategies accordingly.
Advanced Techniques and Tools
For those looking to take their analysis to the next level, there are several advanced techniques and tools available for constructing and interpreting relative frequency distributions. These include statistical software packages, data visualization tools, and advanced statistical methods that can enhance the accuracy and depth of the analysis.
Statistical software packages, such as R, Python, and SPSS, offer powerful capabilities for constructing relative frequency distributions and performing advanced statistical analyses. These tools can handle large data sets, automate calculations, and generate detailed reports and visualizations that facilitate data interpretation.
Data visualization tools, such as Tableau and Power BI, provide intuitive interfaces for creating interactive visualizations that bring relative frequency distributions to life. By using these tools, analysts can create compelling visual representations of their data that enhance understanding and communication.
Case Study Analysis
To illustrate the practical application of constructing a relative frequency distribution of the data, let's consider a case study involving a retail company looking to optimize its product offerings. By analyzing sales data from the past year, the company's analysts constructed a relative frequency distribution to identify which products were most popular among customers.
The distribution revealed that certain products consistently accounted for a significant portion of sales, while others lagged behind. Armed with this information, the company decided to increase its inventory of the top-performing products and reduce its focus on underperforming items. As a result, the company was able to increase sales and improve customer satisfaction by aligning its offerings with customer preferences.
Frequently Asked Questions
What is a relative frequency distribution?
A relative frequency distribution is a statistical tool that represents the proportion or percentage of the total number of occurrences of each category within a data set. It provides insights into the relative importance or prevalence of each category.
How do you construct a relative frequency distribution of the data?
To construct a relative frequency distribution of the data, follow these steps: gather and organize the data, calculate the frequency of each category, determine the total frequency, calculate the relative frequency for each category, and create the distribution table.
Why is relative frequency important?
Relative frequency is important because it provides a standardized measure that allows analysts to compare different data sets or categories. It reveals patterns and trends that may not be apparent from raw data and aids in informed decision-making.
What are some common mistakes to avoid when constructing a relative frequency distribution?
Common mistakes include failing to organize the data properly, overlooking the importance of context, and relying solely on relative frequency distributions for decision-making. Ensuring accuracy and considering the broader context are essential for reliable analysis.
What tools can be used for constructing relative frequency distributions?
Tools such as statistical software packages (R, Python, SPSS) and data visualization tools (Tableau, Power BI) can be used to construct and interpret relative frequency distributions. These tools enhance the accuracy and depth of the analysis.
How can relative frequency distributions be applied in real-world scenarios?
Relative frequency distributions can be applied in various fields, including business, healthcare, and education, to analyze customer behavior, track health outcomes, assess student performance, and more. They provide valuable insights that inform decision-making and strategy development.
Conclusion
Constructing a relative frequency distribution of the data is a powerful skill that enables analysts to unlock the potential within their data sets. By transforming raw data into a meaningful representation of its distribution, analysts can reveal patterns, trends, and insights that drive informed decision-making. Whether you're working in business, healthcare, education, or any other field, the ability to construct a relative frequency distribution empowers you to make data-driven decisions that align with your goals and objectives.
As we've explored throughout this article, the process of constructing a relative frequency distribution involves several key steps, from gathering and organizing data to interpreting the results. By following these steps and avoiding common pitfalls, analysts can ensure the accuracy and reliability of their analysis. Additionally, advanced techniques and tools can further enhance the depth and effectiveness of the analysis, providing a comprehensive view of the data's behavior and implications.
In conclusion, mastering the art of constructing a relative frequency distribution of the data is an invaluable asset in today's data-driven world. By leveraging this skill, you can transform complex data into actionable insights that inform decision-making and drive success. So, embrace the power of data analysis and unlock the potential within your data sets by mastering the art of constructing relative frequency distributions.